In this tutorial, you’re going to learn what is hamming code in computer networks with the help of proper examples.
Let’s get started, Happy learning!
Error Correction in Computer Networks
When the data is transmitted over the network from one host to another, then it can be corrupted or lost during the transmission. The primary function of the data link layer is error control. To control errors, the data link layer uses error detection and error correction techniques.
In computer networking, when the data is transmitted from the sender to the receiver’s side, error detection and correction codes are used to identify the error and correct that error. So that the receiving machine receives the same data which is sent by the sender’s machine.
Types of Error Correction Codes
Based on no. of errors in data, we classify the error correction codes into two types as follows:
- Single bit error correction
- Burst error correction
We use single bit error correction when the single bit of data block is corrupted or lost during the transmission. On the other hand, we use burst error correction when multiple bits of the data are corrupted or lost.
In most communication networks, we use the hamming code for error correction. Hamming code is the best error correction code.
What is Hamming Code in Computer Networks
Hamming code in computer networks is linear block code for error correction and was developed by R.W. Hamming. This mechanism is used to identify and correct errors which can occur during the data transmission. It is possible to detect up to 2 errors and correct only one using hamming code technique.
Hamming code in computer networks is based on the relationship between data bits and redundant bits. For any length of a data unit, we can apply hamming code for error correction and detection.
Redundant Bits
The central concept in detecting or correcting the error is redundancy. To be able to detect or correct errors, we need to add some extra bits to our data.
The sender adds these redundant bits and the receiver removes them at the receiver’s side. The presence of redundant bits allows the users to detect or correct corrupted bits.
The following formula is used to calculate the no. of redundant bits.
2^R = M+R+1
Where R stands for redundant bits and M is the data bits.
Parity Bits
A parity bit is added to the actual data block to make the number of 1’s even or odd. Basically, there are two types of parity bits:
Even Parity: In even parity, an additional bit is added at the end of the data block to make the number of 1’s even. If the no. of 1s are already even in the data, then parity bit 0 is added. If the no. of 1’s are added odd in the data block, then parity bit 1 is added.
Odd Parity: In odd parity, an additional bit is added to make the number of 1’s odd. If the no. of 1’s is already odd in the actual data unit, then parity bit 0 is added, otherwise, parity bit 1 is added.
Algorithm of Hamming Code
The algorithm of the hamming code in computer networks comprises two major steps which are encoding and decoding a message. The data is encoded at the sender’s side and decoded at the receiver’s side.
Encode a message: We encode the message at the sender’s side and then it is transmitted over the network. The following steps are involved in encoding a message.
- Write the bit position in the binary format.
- Calculate the number of redundant bits for a message.
- Do the positioning of redundant bits.
- Then do the calculations and calculate the value of each redundant bit.
- Append the redundant bits with actual data and transmit.
Decode the message: At the destination end, the receiver receives the encoded message and performs the recalculations to calculate the errors. If the message has an error, then these errors are corrected. To perform recalculations following steps are performed.
- Calculate the number of redundant bits using the same formula.
- Do the positioning of redundant bits.
- The parity checking technique is used to check parity bits.
- Perform error detection and correction.
Hamming Code Example
Let’s take a hamming code example of a bit word 1011 is to be transmitted from the sender to the destination machine. Construct the even parity seven-bit hamming code for this data.
The binary format of bits.
Positioning of redundant bits.
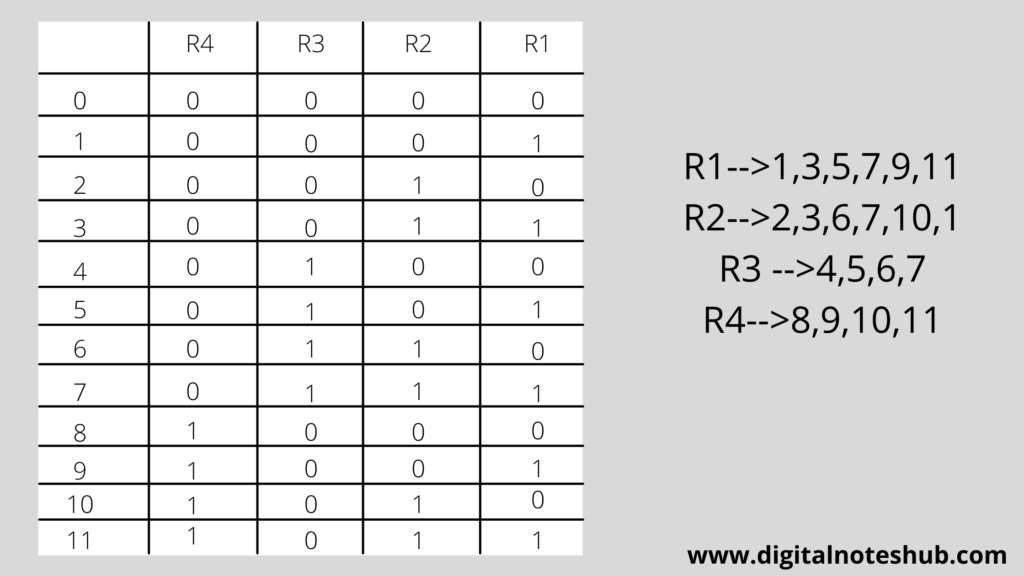
The positions which correspond to the power of 2 are filled with redundant bits. It means at positions 1,2, and 4 redundant bits are placed.
As in the above example, Number of data bits = 4
So the number of redundant of bits = 3
total number of bits to be transmitted = 4+3 = 7
| D7 | D6 | D5 | R4 | D3 | R2 | R1 |
So put the bits into the above code word.
| 1 | 0 | 1 | R4 | 1 | R2 | R1 |
Decide the Redundant bits
We calculate R1 bit using all bit positions whose binary representation includes 1 in the least significant position. It means bits 1,3,5,7 are used to calculate the value of the R1 bit.
We calculate the R2 bit using all the bit positions whose binary representation includes 1 in the second position from the least significant bits. It means bits 2,3,6,7 are used to calculate the value of the R2 bit.
We calculate the R4 bit using all the bit positions whose binary representation includes 1 in the third position from the least significant bits. It means bits 4,5,6,7 are used to calculate the value of the R4 bit.
We have to construct an even parity bit hamming code, as mentioned in the above example.
To calculate the redundant bit, use the even parity checking technique. It means the number 1’s should be even as shown in the example below.

Now we have calculated the valve of redundant bits to fill the value of redundant bits into the corresponding position. So following is the complete codeword to transmit.
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Your thoughts
Have you enjoyed this tutorial on what is hamming code in computer networks? Post your thoughts in the comment section and also try the following tutorials.
